Chiziqli tengsizlikka keltiriladigan bir noma’lumli tengsizliklarni yechish sonli tengsizliklarning 12- § da qaralgan xossalariga asoslangan.

Tengsizliklarni yechishga misollar keltiramiz.

 1 - m a s a l a . Tengsizlikni yeching:

x + 1 > 7 – 2x.

 x son berilgan tengsizlikning yechimi, ya’ni x son x + 1 > 7 – 2x tengsizlikni to`g`ri tengsizlikka aylantiradi, deb faraz qilamiz.

–2x hadni tengsizlikning o`ng qismidan chap qismiga uning ishorasini qarama-qarshisiga o`zgartirgan holda o`tkazamiz, 1 sonini esa tengsizlikning o`ng qismiga “–” ishorasi bilan o`tkazamiz.

Natijada ushbu

 x + 2x > 7 – 1

to`g`ri tengsizlikni hosil qilamiz.

Bu tengsizlikning ikkala qismida o`xshash hadlarni ixchamlaymiz:

3x > 6.

Endi tengsizlikning ikkala qismini 3 ga bo`lib,

x < 2

ekanini topamiz.

Shunday qilib, x ni berilgan tengsizlikning yechimi, deb faraz qilib, biz x > 2 ni hosil qildik. x ning 2 dan katta istalgan tengsizlik qiymati tengsizlikning yechimi bo`lishiga ishonch hosil qilish uchun barcha mulohazalarni teskari tartibda olib borish yetarli.

Aytaylik, x > 2 bo`lsin. To`g`ri sonli tengsizliklarning xossalarini qo`llab, ketma-ket quyidagilarni hosil qilamiz:

3x > 6,

x + 2x > 7 – 1,

x + 1 > 7 – 2x.

binobarin, 2 dan katta istalgan x son berilgan tengsizlikning yechimi no`ladi.

J a v o b .  x > 2.

Tengsizlikning yechilishini yozishda batafsil izohlarni keltirish shart emas. Masalan,      1-masalaning yechilishini bunday yozish mumkin:

x + 1 > 7 – 2x,

3x > 6,

x > 2.

Shunday qilib, tengsizlikni yechishda uning quyidagi xossalaridan foydalaniladi:

Bu xossalar berilgan tengsizlikni boshqa, xuddi shunday yechimlarga ega bo`lgan tengsizlik bilan almashtirishga imkon beradi.

Chiziqli tengsizlikka keltiriladigan bir no`ma’lumli tengsizliklarni yechish uchun:

1) noma’lum qatnashgan hadlarni chap tomonga, noma’lum qatnashmagan hadlarni esa o`ng tomonga o`tkazish (1- xossa);

2) o`xshash hadlarni ixchamlab, tengsizlikning ikkala qismini noma’lum oldidagi koeffitsiyentga (agar u nolga teng bo`lmasa) bo`lish (2- xossa) kerak.

2- m a s a  l a . Tengsizlikni yeching:

3(x – 2) – 4(x + 1) < 2(x – 3) – 2.

 Tengsizlikning chap va o`ng qismlarini soddalashtiramiz. Qavslarni ochamiz:

3x – 6 – 4x – 2 < 2x – 6 – 2.

Noma’lum qatnashgan hadlarni tengsizlikning chap qismiga, noma’lum qatnashmagan (ozod) hadlarni esa o`ng qismiga olib o`tamiz (1- xossa):

3x – 4x – 2x < 6 + 4 – 6 – 2.

O`xshash hadlarni ixchamlaymiz:

–3x < 2.

va tengsizlikning ikkala qismini –3 ga bo`lamiz (2- xossa):

J a v o b .

Bu yechilishni qisqacha bunday yozish mumkin:

3(x – 2) – 4(x + 1) < 2(x – 3) – 2,

3x – 6 – 4x – 2 < 2x – 6 – 2,

– x – 10 < 2x – 8,

–3x < 2,

 tengsizlikni qaqnoatlantiruvchi x sonlar to`plami son o`qida nur bilan tasvirlanadi (29- rasm).  nuqta bu nurga tegishli emas, 29- rasmda u oq doiracha bilan, nur esa qiya chiziqchalar bilan belgilangan.

x sonlarning, masalan, x ≥ 2 tengsizlikni qanoatlantiruvchi to`plami ham nur deyiladi.     x = 2 nuqta shu nurga tegishli. 30-rasmda bu nuqta qaro doiracha bilan tasvirlangan.

 3- m a s  a l a . Tengsizlikni yeching:

  Tengsizlikning ikkala qismini 6 ga ko`paytiramiz:

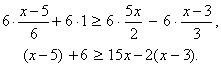
Qavslarni ochamiz va o`xshash hadlarni ixchamlaymiz:

x – 5 + 6 ≥ 15x – 2x +6,

x + 1 ≥ 13x + 6,

bundan

–12x ≥ 5, .

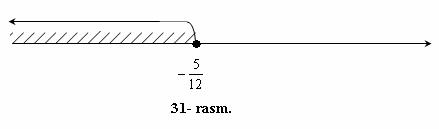
Bu tengsizlikning yechimlari to`plami, ya’ni  sonlar 31- rasmda tasvirlangan.

Qaralgan misollarda tengsizliklar soddalashtirilgandan keyin nom’lum oldida turgan koeffitsiyent nolga teng bo`lmagan chiziqli tengsizlikka keltirildi. Ayrim hollarda bu koeffitsiyent nolga teng bo`lishi mumkin.

Shunday tengsizliklarga misollar keltiramiz.

 4- m a s a l a . Tengsizlikni yeching:

2(x + 1) + 5 > 3 – (1 – 2x).

 Tengsizlikning ikkala qismini soddalashtiramiz:

2x +2 + 5 > 3 – 1 + 2x,

2x +7 > 2 + 2x,

bundan

2x – 2x > 2 – 7,

0 ∙ x > –5.

Oxirgi tengsizlik x ning istalgan qiymatida to`g`ri bo`ladi, chunki chap qismi istalgan       x da nolga teng hamda 0 > –5. Demak, x ning istalgan qiymati berilgan tengsizlikning yechimi bo`ladi.

J a v o b . x – istalgan son.

 5- m a s a l a . Tengsizlikni yeching:

3(2 – x) – 2 > 5 – 3x.

 Tengsizlikning chap qismini soddalshtiramiz

6 – 3x – 2 > 5 – 3x,

4 – 3x > 5 – 3x,

bundan

–3x + 3x > 5 – 4,

0 ∙ x > 1.

Oxirga tengsizlik yechimga ega emas, chunki tengsizlikning chap qismi x ning istalgan qiymatida nolga teng hamda 0 > 1 tengsizlik noto`g`ri. Demak, berilgan tengsizlik yechimga ega emas.

J a v o b .  Yechimlar yo`q.