1. Chiziqli funksiya va uning garafigi
Tekshiriladigan to’g’ri burchakli koordinatalar sistemasi – tanlangan yo’nalishlar va uzunlik birligiga ega bo’lgan ikkita o’zaro perpendikular to’g’ri chiziq.
Bu to’g’ri chiziqlar koordinata o’qlari deyiladi: gorizontal tasvirlangan to’g’ri chiziq – abssissalar o’qi, vertikal tasvirlangan to’g’ri chiziq esa ordinatalar o’qi. Koordinata o’qlarining kesishish nuqtasi koordinatalar boshi deyiladi. Koordinatalar boshi O harfi bian, abssissalar o’qi Ox bilan ordinatalar o’qi Oy bilan belgilanadi.
Koordinata tekisligi – koordinatalar sistemasi tanlangan tekislik.
Funksiya. Agar biror sonlar to’plamida x ning har bir qiymatiga qandaydir qoida bo’yicha y son mos keltirilgan bo’lsa, u holda shu to’plamda funksiya aniqlangan deyiladi.
Bunda x erkli o’zgaruvchi, y (x) esa erksiz o’zgaruvchi yoki funksiya deyiladi.
Chiziqli funksiya, bu y =kx + b ko’rinishidagi funksiyalar, bu yerda k va b – berilgan sonlar.
y(x )funksiyaning grafigi – koordinata tekisligining (x; y (x)) koordinatali barcha nuqtalari to’plami.
Masalan,
y(x)=2x+1
funksiyaning grafigi – koordinata tekisligining (x;
2x+1)
koordinatali barcha nuqtalari to’plami.
y=kx+b chiziqli funksiyaning grafigi – to’g’ri chiziq, b = 0 bo’lgan funksiya y = kx ko’rinishini olad, uning grafigi koordinatalar boshidan o’tadi.
To’g’ri proporsional bog’lanish: y =kx munosabat, bunda k>0, x>0,k – proporsionallik koeffitsiyenti.
Masalan,
s
= vt
formulada tezlik o’zgarmas bo’lganda
s
yo’l t
vaqtga
to’g’ri proporsional.
Teskari
proporsional bog’lanish: 
,
bunda k
> 0, x > 0, k
– proporsionallik koeffitsiyenti.
Masalan,
V=
formuladagazning
V
hajmi m
massa o’zgarmas bo’lganda 
zichlikka
teskari proporsional.
2. Ikki noma’lumli ikkita chiziqli tenglamalar sistemasi
Ikki noma’lumli ikkita chiziqli tenglamalar sistemasining umumiy ko’rinishi quyidagicha:
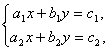
Bu yerda a1, b1, c1, a2, b2, c2, - berilgan sonlar x, y – noma’lum sonlar.
Sestimaning yechimi – shu sestimaga qo’yganda uning har bir tenglamasini to’g’ri tenglikka aylantiruvchi x, y sonlar juftligi.
Masalan,
sistemaning yechimi x = 1, y = 2 sonlar juftligi bo’ladi.
Sistemani yechish uning barcha yechimlarini topish yoki ularning yo`qligini ko`rsatish demakdir.
Tenglamalar sistemasini yechishda bunday usullar qo`llaniladi.
1) O`rniga qo`yish usuli.
Tenglamalardan birida noma’lumlarning biri ikkinchisi orqali ifodalanadi va sistemaning ikkinchi tenglamasiga qo`yiladi.
2) Algebraik qo`shish usuli.
Noma’lumlardan birining oldida turgan koeffisiyentlarning modullarini tenglab, sistema tenglamalarini hadlab qo`shish yoki ayirish orqali shu noma;lum yo`qotiladi.
3) Grafik usuli.
Sistema tenglamalarining grafiklari yasaladi va ularning kesishish nuqtasining koordinatalari topiladi.
3. TENGSIZLIKLAR
a > b tengsizlik a – b ayirma musbat, ya’ni a – b > 0 ekanini bildiradi.
a < b tengsizlik a – b ayirma manfiy, ya’ni a – b < 0 ekanini bildiradi.
Istalgan ikkita a va b son uchun quyidagi uchta muniosabatdan faqat bittasi to`g`ri bo`ladi: a > b a = b a < b.
a va b sonlarni taqqoslash – to`g`ri munosabat hosil bo`lishi uchun bu sonlar orasiga >, <, = belgilaridan qaysinisi qo`yish kerakligini aniqlash demakdir.
Sonli tengsizliklarning asosiy xossalari:
1. Agar a > b bo`lsa, u holda b < a bo`ladi.
2. Agar a > b va b > c bo`lsa, u holda a > c bo`ladi.
3. Agar tengsizlikning ikkala ayni bir songa qo`shilsa yoki ulardan ayni bir son ayrilsa, u holda tengsizlik ishoraso o`zgarmaydi: agar a > b bo`lsa, u holda ixtiyoriy c son uchun
a + c > b + c
va
a – c > b – c
bo`ladi
Istalgan qo`shiluvchini tengsizlikning bir qismidan uning ikkinchi qismiga shu qo`shiluvchining ishorasini qarama-qarshisiga o`zgartirgan holda o`tishi mumkin.
4. Agar tengsizlikning ikkala qismini ayni bir musbat songa ko`paytirilsa yoki bo`linsa, u holda tengsizlik ishorasi o`zgarmaydi. Agar tengsizlikning ikkala qismini ayni bir manfiy songa ko`paytirilsa yoki bo`linsa, u holda tengsizlik ishorasi qarama-qarshisiga o`zgaradi.
Agar a > b bo`lsa, u holda
c
> 0 bo`lganda
ac > bc
va 
bo`ladi,
c
< 0 bo`lganda
ac < bc
va 
bo`ladi.
5. Tengsizliklarni qo`shish. Bir xil ishorali tengsizliklarni qo`shish mumkin, bunda xuddi shu ishorali tengsizlik hosil bo`ladi: a > b va c > d bo`lsa, u holda a +c > b + d bo`ladi.
6. Tengsizliklarni ko`paytirish. Chap va o`ng qismlari musbat bo`lgan bir xil ishorali tengsizliklarni ko`paytirish mumkin, bunda xuddi shu ishorali tengsizlik hosil bo`ladi: agar a > b, c > d va a, b, c va d – musbat sonlar bo`lsa, u holda ac > bd bo`ladi.
7. Tengsizlikni darajaga ko`tarish. Chap va o`ng qismlari musbat bo`lgan tengsizlikni natural darajaga ko`tarish mumkin, bunda xuddi shu ishorali hosiol bo`ladi: agar a > b > 0 bo`lsa, u holda n ning istalgan qiymatida an > bn bo`ladi.
Qat’iy tengsizlik – > (katta) va < (kichik) ishorasiga ega bo`lgan tengsizlik.
Masalan,
5
> 3, x < 1.
Noqat’iy tengsizlik – ≥ (katta yoki teng) va ≤ (kichik yoki teng) ishorasiga ega bo`lgan tengsizlik.
Masalan,
a2
+ b2 ≥ 2ab, x ≤ 3.
a ≥ b noqat’iy tengsizlik a > b yoki a = b ekanini bildiradi, Noqat`iy tengsizliklarning xossalari qat`iy tengsizlik xossalari bilan bir xil. Bunda qat’iy tengsizliklar xossalarida > va < ishoralari, noqat`iy tengsizliklar xossalarida esa ≥ va ≤ ishoralari qarama-qarshi ishoralar deb hisoblanadi.
Bir nomq’lumli tengsizlik – harf bilan belgilangan noma’lum sonni o`z ichiga olgan tengsizlik.
Bir noma’lumli tengsizliklarga misollar:
3x + 4 < 5x
– 2;
Bir noma’lumli tengsizlikning yechimi – noma’lumning berlgan tengsizlikno to`g`ri sonli tengsizlikka aylantiradigan qiymati.
Tengsizlikni yechish uning hamma yechimlarini topish yoki ularning yo`qligini topish demakdir.
Bir noma’lumli tengsizliklar sistemasi – ayni bir noma’lum sonni o`z ichiga olgan va birgalikda qaraladigan bir nechta tengsizlik.
Bir noma’lumli tengsizliklar sistemasiga misollar:
Tengsizliklar sistemasining yechimi – noma’lumning sistema barcha tengsizliklarini to`g`ri sonli tengsizlikka aylantiradigan qiymati.
Masalan,
2
soni
sistemaning yechimi bo`ladi, chunki 3 ∙ 2 – 4 < 2, 2 + 2 > 3 – to`g`ri tengsizliklar.
Tengsizliklar sistemasini yechish uning barcha yechimlarini topish yoki ularning yo`qligini aniqlash demakdir.
Sonli oraliqlar – kesmalar, intervallar, yarim intervallar.
[a; b] kesma, bu a ≤ x ≤ b tengsizliklarni qanoatlantiruvchi x sonlar to`plami, bunda a < b.
Masalan,
[2;
5]kesma, bu
2 ≤ x
≤ 5
tengsizliklarni qanoatlantiruvchi
x
sonlar
to`plami.
(a; b) interval bu a < x < b tengsizliklasni qanoatlantiruvchi x sonlar to`plami, bunda a < b.
Masalan,
(–2,
3) interval,
bu –2 < x
< 3
tengsizliklarni qanoatlantiruvchi
x
sonlar to`plami.
[a; b) yarim interval, bu a ≤ x < b tengsizliklarni qanoatlantiruvchi x sonlar to`plami; (a; b] yarim interval, bu a < x ≤ b tengsizliklarni qanoatlantiruvchi x sonlar to`plami, bunda a < b.
Masalan,
[3,
8) yarim
interval 3 ≤
x < 8
tengsizliklarni qanoatlantiruvchi
x
sonlar to`plami;
(–4, 2)
yarim interval
–4 ≤ x < 2
tengsizliklarni qanoatlantiruvchi x sonlar to`plami.
a sonning moduli (|a| kabi belgilanadi) bunday formula bilan aniqlanadi:
Geometrik nuqtayi nazardan |a|, bu 0 nuqtadan a sonni tasvirlovchi masofa.
Istalgan a son uchun |a| > 0 tengsizlik bajariladi, bunda faqat a = 0 bo`lganda va faqat shundagina |a| = 0 bo`ladi.
|x| ≤ a tengsizlikni [–a; a] intervaldagi nuqtalar, ya’ni –a ≤ x ≤ a bo`ladigan x sonlar qanoatlantiradi, bunda a>0
|x|< a tengsizlikni (- a; a) intervaldagi nuqtalar, ya’ni – a < x < a bo’ladigan x sonlar qanoatlantiradi, bunda a>0.
|x| ≥ a tengsizlikni barcha x ≤ – a va x ≥ a sonlar qanoatlantiradi, bunda a > 0.
|x |> a tengsizlikni barcha x< –a va x > a sonlsr qanoatlantirad, bunda a > 0
4. Taqribiy hisoblashlar
Yaqinlashiahning absolut xatoligi – miqdorning (kattalikning ) aniq qiymati bilan uning taqribiy qiymati ayirmasining modili. Agar a taqribiy qiymat, x esa aniq qiymat bo’lsa, u holda absolut xatolik |x – a| ga teng.
x = a ± h yozuv yaqinlashishning absolut xatoligi h dan ortiq emasligini, ya’ni |x – a| ≤ h yoki a – h ≤ x ≤ a + h ekanini bildiradi.
Bunda x son a ga h gacha aniqlikda teng deyiladi. Masalan, π = 3,14 ±0,01 yozuvi | π – 3,14| ≤0,01 ekanini ya’ni π soni 3,14 ga 0,01 gacha aniqlikda tengligini bildiradi.
Sonni 10-n gacha aniqlikda kami bilan yaxlitlashda verguldan keyingi dastlabki n ta raqam qoldirilib, qoldirilib, qolganlari tashlab yuboriladi.
Masalan,
17,2397
sonini mingdan birgacha, ya,ni
10-3
gacha kami bilan yaxlitlashda
17,239
ni yuzdan birgacha yaxlitlashda
17,23
ni; o’ndan birgacha yaxlitlashda
17,2
ni hosil qilamiz.
Sonni 10-n gacha aniqlikda ortig’i bilan yaxlitlashda verguldan keyingi n – raqam bir birlik orttiriladi va undan keyingi barcha raqamlar tushirib qoldiriladi.
Masalan,
2,5143
sonini mingdan birgacha ortig’i bilan yaxlitlashda
2,515
ni; yuzdan bargacha yaxlitlashda
2,52
ni; o’ndan birgacha yaxlitlashda
2,6
ni hosil qilamiz.
Ikkala holda ham yaxlitlash xatoligi 10-n dan oshib ketmaydi.
Eng kam xatoli yaxlitlash: agar berilgan sondagi tashlab yuboriladigan birinchi raqam 5 dan kichik bo’lsa, u holda kami bilan yaxlitlanadi; agar bu raqam 5 dan katta yoki unga teng bo’lsa, u holda ortig’I bilan yaxlitanadi.
Masalan,
8,351
sonini yuzdan birgacha aniqlikda yaxlitlashda
8,35
ni; o’ndan birgacha aniqlikda yaxlitlashda esa
8,4
ni hosil qilami.
x ≈ a yozuvi a son x sonning taqribiy qiymati ekanini bildiradi.
Masalan:
Nisbiy xatolik – absolut xatolikni miqdor (kattalik)ning taqribiy qiymati moduliga bo’lish natijasi. Agar x – aniq qiymat, a – taqribiy qiymat bo’lsa, u holda nisbiy xatolik quyidagiga teng:
Nisbiy xatolik odatda protsentlarda ifodalanadi.
Masalan,
agar
miqdorning aniq qiymati
1,95
ga teng, taqribiy
qiymati esa 2
ga teng bo’lsa, u holda yaqinlashishning nisbiy hatoligi quyidagiga teng:
5. Kvadrat ildizlar
a soning kvadrat ildizi − kvadrati a ga teng bo’lgan son.
Masalan,
6
soni 36
ning kvadrat ildizi; −
6
soni ham 36
sonining kvadrat ildizi.
Kvadrat ildiz chiqarish − kvadrat ildizni topish amali. Faqat nomanfiy sondangina kvadrat ildiz chiqarish mumkin.
a
sonning
arifmetik kvadrat ildizi
− kvadrati
a
ga teng
bo’lgan nomanfiy son. Bu son quyidagicha belgilanadi:
.
Masalan: 
ifoda
faqat a ≥
0
bo’lgandagina
ma’noga ega, bunda ≥
0,
()2
= a
Ayniyat − unga kiruvchi harflarning istalgan qiymatlarida o’rinli bo’lgan tenglik.
=
|a|
tenglik
ayniyat bo’ladi, chunki u
a
ning istalgan qiymatlarida bajariladi.
Masalan,
Agar
a > b > 0
bo’lsa, u holda >
bo’ladi.
Masalan,
,
chunki 17>13>0.
Kvadrat ildizlarning xossalari:
1)
agar
Masalan:
2) agar
Masalan:
3) Ko’paytuvchini ildiz ostidan chiqarish:
Agar
a
≥ 0, b>0
bo’lsa, u holda 
bo’ladi.
4) Ko’paytuvchini ildiz belgisi ostiga kiritish:
Agar
a ≥ 0, b ≥ 0
bo’lsa, U holda 
bo’ladi.
Ikki musbat a va b
sonning o’rta geometrigi esa 
sondir.
Ikki musbat sonning o’rta arifmetigi shu sonlarning o’rta geometrigidan kichik emas:
Agar
a> 0, b> 0
bo’lsa, u holda 
bo’ladi.
Ratsional son,
bu
ko’rinishidagi
son, bunda m
− butun son,
n − natural
son.
Ratsional sonni chekli o’nli kasr yoki cheksiz davriy o’nli kasr shaklida tasvirlash mumkin.
Masalan,
Irratsional son – cheksiz nodavriy o`nli kas.
Masalan,
0,1001000100001….
Ratsional va irratsional sonlar birgalikda haqiqiy sonlar to`plamini tashkil qiladi.
Har bir irratsional sonni taqriban chekli o`nli kasr bilan, ya’ni ratsional son bilan almashtirish mumkin.
Masalan,
π
sonini taqriban
3,14
ratsional soni bilan, 
sonini
taqriban 1,41
ratsional son bilan almashtirish mumkin.
Amalda irratsional son bilan hisoblashlarda ularning ratsional yaqinlashishlari yordamida bajariladi.
Masalan,
bo`lgani
uchun 
bo`ladi.
Kvadrat ildizlarni taqriban topish uchun jadvak yoki hisoblash mashinalaridan foydalaniladi.
6. Kvadrat tenglamalar
Kvadrat tenglama – ushbu
ax2 + bx + c = 0
ko`rinishdagi tenglama, bunda a, b va c – berilgan sonlar, a ≠ 0, x – noma’lum son.
Kvadrat tenglamaning koeffitsiyentlari bunday ataladi: a – birinchi yoki bosh koeffitsiyent, b – ikkinchi koeffitsiyent, c – ozod had.
Kvadrat tenglamaga misollar: 2x2 – x – 1 = 0, 3x2 + 7 = 0.
Chala kvadrat tenglama, bu b yoki c koeffitsiyentlaridan bittasi nolga teng bo`lgan
ax2 + bx + c = 0
kvadrat tenglama.
Chala kvadrat tenglamalarga misollar: x2 = 0, 5x2 + 4 = 0, 8x2 + x = 0.
x2
= d
ko`rinishdagi tenglama, bunda
d
> 0, ikkita
haqiqiy 
ildizga
ega. Agar
d = 0
bo`lsa, u
holda x2
= 0 tenglama
bitta x
= 0 ildizga (ikkita
teng ildizga) ega.
Agar d < 0 bo`lsa, u holda x2 = 0 tenglama haqiqiy ildizga ega emas.
ax2 + bx + c = 0 kvadrat tenglama, bunda a, b va c – haqiqiy sonlar, ushbu
bunda
b2
– 4ac ≥ 0
formula bilan topiladigan x1, x2 ildizlarga ega.
Masalan:
1 3x2 + 5x – 2 = 0 tenglama ikkita haqiqiy ildizga ega:
ya’ni
2) 4x2 – 6x + 25 = 0 tenglama esa haqiqiy ildizga ega emas, chunki
b2 – 4ac = 36 – 4 ∙ 4 ∙ 25 < 0.
Keltirilgan kvadrat tenglama, bu x2 + px +qc = 0 ko`rinishdagi tenglama.
Keltirilgan kvadrat tenglama ildizlari formulasi:
bunda
Masalan,
x2
– 6x – 7 = 0
tenglamaning haqiqiy ildizlari bunday:
ya’ni x1 = 7, x2 = –1.
Viyet teoremasi. Keltirilgan kvadrat tenglama ildizlarining yig`indisi qarama-qarshi ishora bilan olingan ikkinchi koeffitsiyentga, ularning ko`paytmasi esa ozod hadgateng: agar x1 va x2 ushbu x2 + px +q = 0 tenglamaning ildizlari bo`lsa, u holda x1 + x2 = –p, x1x2 = q bo`ladi.
Viyet teoremasiga teskari teorema. Agar p, q, x1 va x2 sonlar uchun x1 + x2 = –p, x1x2=q munosabatlar bajarilsa, u holda x1 va x2 ushbu x2 + px +q = 0 tenglamaning ildizi bo`ladi.
Kvadrat uchhad, bu ax2 + bx + c ko`rinishdagi ko`phad, bunda a ≠ 0.
Kvadrat uchhadni ko`paytuvchilarga ajratish uni
ax2 + bx + c =a(x – x1)(x – x2)
ko`rinishdagi tasvirlash demakdir, bunda x1 va x2 lar ax2 + bx + c = 0 kvadrat tenglamaning ildizlari.
Masalan,
