VII   SINF   ALGEBRA   KURSINING   QISQACHA   MAZMUNI

 

1.                                Algebraik  ifodalar

 

Sonli ifoda – sonlardan tuzilib, amallar belgilari bilan birlashtirilgan yozuv.

Masalan, 1,2·(–3)– 9:0,5 – sonli ifoda.

Algebrada harflardan har xil sonlarni belgilash uchun foydalaniladi.

Masalan, agar 2(n+m) tomonlari n va m bo‘lgan to‘g‘ri to‘rtburchakning perimetri bo‘lsa, u holda n va m harflari o‘rnida istalgan musbat sonlar tushuniladi.

Algebraik ifoda – bu sonlar va harflardan tuzilib, amallar bel­gilari bilan birlashtirilgan ifodalar.

Algebraik ifodalarga misollar:

2(m+ï);  3a+2ab–1;  (a–b)2; .

 

Algebraik ifodaning son qiymati – berilgan ifodadagi harflarni sonlar bilan almashtirilgandan keyin hisoblash natijasida hosil bo‘l­gan son.

Masalan, 3à+2ab–1 ifodaning son qiymati a=2 va b=3 bo‘lganda 3·2+2·2·3–1=17 ga teng bo‘ladi.

a sonning n natural ko‘rsatkichli darajasi – bu har biri a ga teng bo‘lgan n ta ko‘paytuvchi ko‘paytmasidir, ya’ni

.

Masalan,

.

 

   an  darajaning yozuvida a soni – daraja asosi, n son – daraja ko‘rsatkichi.

Masalan,     22 yozuvida 2 soni - darajaning asosi, 3 soni – daraja ko‘rsatkichi.

Sonning birinchi darajasi sonning o‘zidir:  a1=a.

Masalan, 31 = 3, ()1 =.

 

Sonning kvadrati – bu shu sonning 2 ko‘rsatkichli darajasidir. Masalan, 52 –bu 5 sonining kvadrati.

Sonning kubi – shu sonning 3 ko‘rsatkichli darajasidir. Masalan, 43 – bu 4 sonining kubidir.

 

Darajaning asosiy xossalari.

1)       Bir xil asosli darajalarni ko‘paytirishda asos o‘zgarishsiz qola­di, daraja ko‘rsatkichlar esa qo‘shiladi:

a n  · a m  = a n + m.

 

2)      Bir xil asosli darajalarni bo‘lishda asos o‘zgarishsiz qoladi, daraja ko‘rsatkichlar esa ayiriladi:

an : am = a n –  m .

 

3)       Darajani darajaga ko‘tarishda asos o‘zgarishsiz qoladi, daraja ko‘rsatkichlar esa o‘zaro ko‘paytiriladi:

( an )m = a nm .

 

4)      Ko‘paytmani darajaga ko‘tarishda har bir ko‘paytuvchi shu darajaga ko‘tariladi:

(a· b)n= an · bn.

 

5) Kasrni  darajaga  ko‘tarishda  uning  surat  va  maxraji  shu darajaga ko‘tariladi:

() n = .

 

Amallarni bajarish tartibi.

Birinchi bosqich amallar - qo‘shish va ayirish.

lkkinchi bosqich amallar - ko‘paytirish va bo‘lish.

Uchinchi bosqich amallar - darajaga ko‘tarish.

1) Agar ifoda qavslami o‘z ichiga olmagan bo‘lsa, u holda avval uchinchi bosqich amallar, so‘ngra ikkinchi bosqich amallar va nihoyat, birinchi bosqich amallar bajariladi; bunda bir xil bosqich amallar ular qanday tartibda yozilgan bolsa, xuddi shunday tartibda bajariladi.

2)    Agar ifoda qavslami o‘z ichiga olgan bo‘lsa, u holda avval qavslar ichidagi sonlar ustidagi barcha amallar, keyin esa qolgan barcha amallar bajariladi: bunda qavs ichidagi sonlar ustidagi amallarni va qavsdan tashqaridagi amallarni 1- bandda ko‘rsatilgan tartibda olib boriladi.

3)    Agar kasr ifodaning qiymati hisoblanayotgan bo‘lsa, u holda kasrning suratidagii amallar va maxrajidagi amallar bajariladi va birinchi natija ikkinchisiga bo‘linadi.

4)  Agar ifoda boshqa qavslar ichida joylashgan qavslami o‘z ichiga olgan bo‘lsa, u holda avval ichkaridagi qavslar ichidagi amal­lar bajariladi.

Algebraik yig‘indi – bir necha algebraik ifodalardan tuzilib, «+» yoki «-» ishoralari bilan birlashtirilgan yozuvlardir.

 

Qavslami ochish qoidalari.

1)      Agar algebraik ifodaga qavs ichida turgan algebraik yig‘indi qo‘shilgan bo‘lsa, u holda shu algebraik yig‘indining har bir
qo‘shiluvchisi oldida turgan ishoralarni saqlagan holda qavslami tushirib qoldirislrmumkin, masalan:

14 + (7–23 + 21)= 14 + 7–23 + 21.

a + (b–c–d)=a + b–c–d.

2)      Agar algebraik ifodadan qavs ichida turgan algebraik ifodani ayiriladigan bo‘lsa, u holda shu algebraik yig‘indining har bir
qo‘shiluvchisi oldida turgan ishoralarni qarama-qarshisiga o‘zgartirilgan holda qavslami tushirib qoldirish mumkin, masalan:

14–(7–23 + 21)=14–7 + 23–21.

a – (b – c – d) = a – b + c + d.

 

 

2.               Birhadlar  va  ko‘phadlar

 

Birhad – son va harfiy ko‘paytuvchilar ko‘paytmasidan iborat al­gebraik ifoda.

Birhadlarga misollar:  3ab, –2ab2c3,  a2,  a,  0,6 xy5y2, –t4.

Masalan,  ushbu

3a2·(0,4) ·b(–5)c2

birhadning sonli ko‘paytuvchilari 3; 0,4; –5, harfiy ko‘paytuvchilari esa a2, b,         c2 bo‘ladi.

Standart shakldagi birhad birinchi o‘rinda turuvchi faqat bitta sonli ko‘paytuvchidan va turli harfiy asosli darajalardan tuzilgan birhad.

Birhadni standart shaklda yozish uchun uning barcha son ko‘paytuvchilarini o‘zaro ko‘paytirish va ularning ko‘paytmasini birin­chi o‘ringa qo‘yish, so‘ngra barcha bir xil harfiy ko‘paytuvchilarni daraja shaklida yozish kerak.

Birhadning koeffitsienti standart shaklida yozilgan birhadning sonli ko‘paytuvchisi. Masalan, abc2   birhadning koeffitsienti  ga teng, –7a2b birhadning koeffitsienti –7 ga teng, a2bc birhadning koeffitsienti 1 ga teng, –ab2 birhadning koeffitsienti –1 ga teng.

Ko‘phad bir nechta birhadning algebraik yig‘indisi.

Ko‘phadlarga misollar:   4ab2c  – birhad,

   2ab–3bc  – ikkihad,

       4ab+3ac–bc  – uchhad.

Ko‘phadning hadlari ko‘phadni tashkil qiluvchi birhadlardir. Masalan, 2àb2–3à2b+7àñ–4bñ ko‘padning hadlari 2ab2, –3à2b, 7ac, –4bc bo‘ladi.

O‘xshash hadlar – faqat koeffitsientlari bilan farq qiluvchi birhadlar yoki bir xil birhadlar.

O‘xshash hadlarni ixchamlash ko‘phadni soddalashtirish bo‘lib, bunda o‘xshash birhadlarning yig‘indisini bitta birhad bilan al-mashtiriladi. Masalan,

2ab–4bc + ac+3àb+bc=5ab–3ab+ac.

Ko‘phadning standart shakli – barcha hadlari standart shaklda yozilgan va ularning orasida o‘xshashlari o‘lmagan ko‘phadning yozuvi.

 

Birhadlar va ko‘phadlar ustida amallar.

1) Bir nechta ko‘phadlar algebraik yig‘indisini ko‘phadning stan­dart shaklida yozish uchun qavslarni ochish va o‘xshash hadlarni ixchamlash kerak, masalan:

(2a2b–3bc)+ (a2b+5bc)–(3a2b–bc)=2a2b–3bc+a2b+5bc+3a2b+bc=3bc.

2) Ko‘phadni birhadga ko‘paytirish uchun ko‘phadning har bir hadini shu birhadga ko‘paytirish va hosil bo‘lgan ko‘paytmalarni qo‘shish kerak, masalan:

(2ab–3bc)(4ac)=(2ab)(4ac)+(–3bc)(4ac)=8a2bc–12abc2.

3)      Ko‘phadni ko‘phadga ko‘paytirish uchun birinchi ko‘phad­ ning har bir hadini ikkinchi ko‘phadning har bir hadiga ko‘paytirish
va hosil bo‘lgan ko‘paytmalarni qo‘shish kerak, masalan:

(5a –2b)(3à + 4b) = (5a) (3à) + (5a) (4b) + (–2b)(3a)+(–2b)(4b)=15a2+14ab–8b2.

4)      Ko‘phadni birhadga bo‘lish uchun ko‘phadning har bir hadini shu birhadga bo‘lish va hosil bo‘lgan natijalarni qo‘shish kerak,
masalan:

(4a2b2–12a2b2): (2ab)=(4a2b2):(2ab)+(–12a2b3):(2ab)=2a2b–6ab2.

 

 

3.               Birinchi  darajali  bir  noma’lumli  tenglama

 

Tenglama harf bilan belgilangan noma’lum son qatnashgan tenglik.

Tenglamaga misol: 2x+3=Çx+2, bu yerda x - topilishi kerak bo‘lgan noma’lum son.

Tenglamaning ildizi - noma’lumning tenglamani to‘g‘ri tenglikka aylantiradigan qiymati.

Masalan, 3 soni x+l=7–x tenglamaning ildizi bo‘ladi, chunki 3+1=7–3.

Tenglamani yechish uning barcha ildizlarini topish yoki ularning yo‘qligini aniqlash demakdir.

 

Tenglamaning asosiy xossalari:

1.        Tenglamaning istagan hadini uning bir qismidan ikkinchi qismiga ishorasini qarama-qarshisiga o‘zgartirib olib o‘tish mumkin.

2.    Tenglamaning ikkala qismini nolga teng bo‘lmagan bir xil songa ko‘paytirish yoki bo‘lish mumkin.

 

 

4.  Qisqa  ko‘paytirish  formulalari

 

(a+b)2 = a2 + 2 ab + b2,     a3 + b3= (a + b)(a2– ab + b2),

(a–b)2=a2–2 ab+ b2,     a3 – b3=(a–b)(a2+ ab+ b2),

a2 – b2 =(a+b)(a–b).

 

 

5.  Ko‘phadni  ko‘paytuvchilarga  ajratish

 

Ko‘phadni ko‘paytuvchilarga ajratish - ko‘phadni ikki yoki undan ortiq ko‘phadlar ko‘paytmasi shaklida ifodalashdir, masalan:

4x2 – 9y2 = (2x + 3y)(2x–3y).

Ko‘phadni ko‘paytuvchilarga ajratishda quyidagi usullardan foydalaniladi:

1)      Umumiy ko‘paytuvchini qavsdan tashqariga chiqarish, masalan:

3ax + 6ay = 3a(x + 2y).

2)      Guruhlashu suli, masalan:

    a3–2a2–2a+4=(a3–2a2)­–(2a–4)=a2(a–2)–2(a–2)=(a–2)=(a–2)(a2–2)

yoki

a2–2a2–2a +4 =(a3–2a)–(2a2– 4)= a(a2–2)–2(a2–2)=(a2–2)(a–2).

3)     Qisqa ko‘paytirish formulalarini qo‘llash, masalan:
1) 9x2–y2=(3x+)(3x–);

                  2) 27x3 + 8y6= (3x + 2y2 )(9x2–6xy2+9y4);

                  3) z2 –14z + 49 = (z–7)2.

 

 

6.  Algebraik  kasrlar

 

Algebraik kasr  – surat va maxraji algebraik ifodalar bo‘lgan kasr. Algebraik kasrlarga misollar: .

Algebraik kasr yozuvida harflar faqat shu kasrning maxraji nolga teng bolmaydigan qiymatlarni qabul qilishi mumkin, deb faraz qilinadi.

Kasrlarning asosiy x î ss a si: kasrning surat va maxraji-ni bir xil algebraik ifodaga ko‘paytirish natijasida unga teng kasr hosil bo‘ladi.

Masalan: .

 

Kasrning asosiy xossasidan foydalanib, algebraik kasrning surat va maxrajini umumiy ko‘paytuvchiga qisqartirish mumkin.

Masalan: .

 

Algebraik kasrlarni qo‘shish va ayirish sonli kasrlar uchun qo‘llaniladigan qoidalar bo‘yicha olib boriladi.

Ikki yoki bir necha kasrlarning algebraik yig‘indisini topish uchun bu kasrlar umumiy maxrajga keltiriladi va bir xil maxrajli kasrlarni qo‘shish qoidalaridan foydalaniladi.

Masalan,  va  kasrlarning umumiy maxraji a2b2 ga teng, shuning uchun .

 

Algebraik kasrlarni ko‘paytirish va bo‘lish sonli kasrlar uchun qollaniladigan qoidalar bo‘yicha olib boriladi, masalan:

.

 

 

 

VIII   SINF   ALGEBRA   KURSI

 

7.  Chiziqli  funksiya  va  uning  grafigi

 

Agar x ning biror sonlar to‘plamidagi har bir qiymatiga biror qoida bo‘yicha yson mos qo‘yilsa, u holda shu to‘plamda funksiya aniqlangan deb aytiladi.

Bunda x erkli o‘zgaruvchi, y(x) esa erksiz o‘zgaruvchi yoki funksiya deyiladi.

Chiziqli funksiya

y = kx + b

ko‘rinishdagi funksiyadir, bu yerda k  va b  – berilgan sonlar.

Funksiyani ko‘rsatmali tasvirlash uchun uning to‘g‘ri burchakli koordinatalar sistemasidagi grafigidan foydalaniladi.

Tekislikda to‘g‘ri burchakli koordinatalar sistemasi – tanlangan yo‘nalishlar va uzunlik birligiga ega bo‘lgan ikkita o‘zaro perpendikulyar to‘g‘ri chiziq.

Bu to‘g‘ri chiziqlarni koordinata o‘qlari deyiladi: gorizontal tasvirlangan to‘g‘ri chiziq – abssissalar o‘qi, vertikal tasvirlangan to‘g‘­ri chiziq esa ordinatalar o‘qi.

Koordinata o‘qlarining kesishish nuqtasi koordinatalar boshi deyiladi. Koordinatalar boshini Î harfi bilan, abssissalar o‘qini Ox harfi bilan, ordinatalar o‘qini Oy bilan belgilanadi.

Koordinata tekisligi koordinatalar sistemasi tanlangan tekislikdir.

y(x) funksiyaning grafigi koordinata tekisligining (x; y(x)) koor-dinatali barcha nuqtalari to‘plamidir.

Masalan, y(x)=2x+1 funksiyaning grafigi koordinata tekisligi­ning (x, 2x+1) koordinatali barcha nuqtalari to‘plamidir.

y=kx+b chiziqli funksiyaning grafigi to‘g‘ri chiziqdir. b=0 bolganda funksiya y=kx ko‘rinishini oladi, uning grafigi koordina­talar boshidan o‘tadi.

 

 

8. Birinchi darajali ikki noma’lumli ikki tenglama sistemasi

 

Birinchi darajali ikki noma’lumli ikki tenglama sistemasining umumiy ko‘rinishi quyidagicha:

 

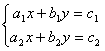
bu yerda a1 , b1, ñ1,  à2, b2, c2 – berilgan sonlar,  x, ó – noma’lum sonlar.

Sistemaning yechimi – shu sistemaga qo‘yganda uning har bir tenglamasini to‘g‘ri tenglikka aylantiruvchi x, ó sonlar jufti.

sistemaning yechimi x =1, y=2 sonlar jufti bo‘ladi.

Sistemani yechish uning barcha yechimlarini topish yoki ular-ning yo‘qligini ko‘rsatish demakdir.

Tenglamalar sistemasini yechishda bunday usullar qo‘llaniladi.

l)O‘rniga qo‘yish usuli.

Tenglamalarning biridan noma’lumlarning birini ikkinchi noma’­lum orqali ifodalanadi va uni sistemaning ikkinchi tenglamasiga qo‘yiladi.

2)Algebraik qo‘shish usuli.

Noma’lumlardan birining oldida turgan koeffitsientlarning mo-dullarini tenglab, sistema tenglamalarini hadlab qo‘shish va ayirish orqali shu noma’lum yo‘qotiladi.

3)Grafik usul.

Sistema tenglamalarning grafiklari yasaladi va ularning kesishish nuqtasining koordinatalari topiladi.