![]()
Funksiyaga doir yana bitta misol keltiramiz.
Asosi 3 ga, balandligi esa x ga teng bo‘lgan to‘g‘ri to‘rtburchakning yuzini hisoblaymiz. Agar izlanayotgan yuzni y harfi bilan belgilansa, u holda javobni y=3x formula bilan yozish mumkin.
![]()
Agar to‘g‘ri to‘rtburchakning asosi k ga teng bo‘lsa, u holda x balandlik bilan y yuz orasidagi bog‘liqlik y=kx formula bilan ifodalanadi. k sonning har bir qiymati biror
(1)
funksiyani aniqlaydi.
Endi y=kx funksiyaning grafigini yasaymiz.
k=2 bo‘lsin, deylik. U holda funksiya bunday ko‘rinishga ega bo‘ladi
y=2x. (2)
x ga turli qiymatlar berib, (2) formula bo‘yicha y ning mos qiymatlarini hisoblaymiz.
![]() Masalan,
x=2
ni olib,
y=4
ni hosil qilamiz. Koordinatalari
(2; 4)
bo‘lgan nuqtani yasaymiz. Agar
x=0
bo‘lsa, u holda
y=2·0=0;
agar
x=–3
bo‘lsa, u holda
y=2·(–3)=–6;
agar
x=0,5
bo‘lsa, u holda
y=2·0,5=1
bo‘ladi va hokazo.
Masalan,
x=2
ni olib,
y=4
ni hosil qilamiz. Koordinatalari
(2; 4)
bo‘lgan nuqtani yasaymiz. Agar
x=0
bo‘lsa, u holda
y=2·0=0;
agar
x=–3
bo‘lsa, u holda
y=2·(–3)=–6;
agar
x=0,5
bo‘lsa, u holda
y=2·0,5=1
bo‘ladi va hokazo.
Jadval tuzamiz:
|
x |
2 |
0 |
-3 |
0,5 |
|
y |
4 |
0 |
-6 |
1 |
Topilgan koordinatalar bo‘yicha nuqtalarni yasaymiz.
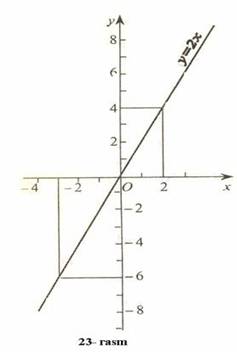
Chiziqni qo‘yib, barcha topilgan nuqtalar koordinatalar boshidan o‘tuvchi bir to‘g‘ri chiziqda yotishga ishonch hosil qilish mumkin. Shu to‘g‘ri chiziq y=2x funksiyaning grafigi bo‘ladi (8-rasm).
Koordinatalari
(x;
y)
bo‘lgan nuqta faqat
y=2x
tenglik to‘g‘ri bo‘lgan holdagina shu to‘g‘ri chiziqda yotadi.
![]() Masalan,
(–1; –2)
koordinatali nuqta to‘g‘ri chiziqda yotadi, chunki
(–2)=2·(–1)
to‘gri tenglik.
Masalan,
(–1; –2)
koordinatali nuqta to‘g‘ri chiziqda yotadi, chunki
(–2)=2·(–1)
to‘gri tenglik.
|
|
y=kx funksiyaning grafigi k ning istagan qiymatida koordinatalar boshidan o‘tuvchi to‘g‘ri chiziq bo‘ladi. Geometriya kursidan ma’lumki, ikki nuqta orqali birgina to‘g‘ri chiziq o‘tadi, shu sababli y=kx funksiyaning grafigini yasash uchun grafikning ikkita nuqtasini yasash yetarli, so‘ngra esa shu nuqtalar orqali chizg‘ich yordamida to‘g‘ri chiziq o‘tkaziladi. Koordinatalar boshi y=kx funksiyaning grafigiga tegishli bo‘lgani sababli bu grafikni yasash uchun uning yana bir nuqtasini topish yetarli. |
![]() M
a s a l a .
y=kx
funksiyaning: 1)
k=1;
2)
k=–1;
3)
k=0
bo‘lgandagi grafigini yasang.
M
a s a l a .
y=kx
funksiyaning: 1)
k=1;
2)
k=–1;
3)
k=0
bo‘lgandagi grafigini yasang.
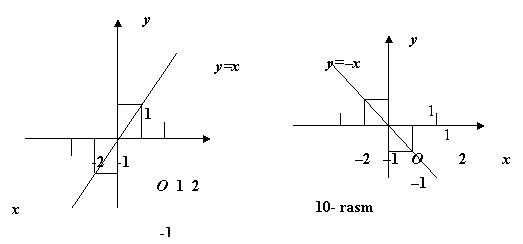
1) k=1 bo‘lganda funksiya y=x ko‘rinishga ega bo‘ladi. Agar x=1 bo‘lsa, U holda y=1 bo‘ladi. Va shuning uchun (1; 1) nuqta grafikka tegishli bo‘ladi. y=x funksiyaning grafigini yasash uchun (0; 0) va (1; 1) nuqtalardan o‘tuvchi to‘g‘ri chiziq chizamiz. Bu to‘g‘ri chiziq birinchi va uchunchi koordinata burchaklarini teng ikkiga bo‘ladi (9-rasm).
2) k=–1 bo‘lganda funksiya y=–x ko‘rinishga ega bo‘ladi. Agar x=1 bo‘lsa, u holda y=–1 bo‘ladi, shuning uchun (1; –1) nuqta grafikka tegishli bo‘ladi. (0; 0) va (1; 1) nuqtalardan o‘tuvchi to‘g‘ri chiziq y=–x gunksiyaning grafigi bo‘ladi (10-rasm).
Bu to‘g‘ri chiziq ikkinchi va to‘rtinchi koordinata burchaklarini teng ikkiga bo‘ladi (10-rasm).
3)
k=0
bo‘lganda funksiya
y=0·x,
ya’ni
y=0
ko‘rinishga ega bo‘ladi. Bu grafikning barcha nuqtalarining ordinatalari nolga
tengligini bildiradi. Shuning uchun bu funksiyaning grafigi abssissalar o‘qi
bilan ustma-ust tushuvchi to‘g‘ri chiziq bo‘ladi. ![]()
|
|
x bilan y orasidagi y=kx formula bilan ifodalangan (bu yerda k>0) bog‘lanishni odatda to‘g‘ri proporsional (mutanosib) bog‘lanish, k sonni esa proporsionallik koeffitsiyenti deyiladi. |
![]() Masalan,
jism o‘zgarmas tezlik bilan harakat qilganda uning bosib o‘tgan yo‘li harakat
vaqtiga to‘g‘ri proporsional. Zichligi doimiy bo‘lgan gazning massasi uning
hajmiga to‘g‘ri proporsional.
Masalan,
jism o‘zgarmas tezlik bilan harakat qilganda uning bosib o‘tgan yo‘li harakat
vaqtiga to‘g‘ri proporsional. Zichligi doimiy bo‘lgan gazning massasi uning
hajmiga to‘g‘ri proporsional.
 TAYANCH TUSHUNCHALAR:
TAYANCH TUSHUNCHALAR:
y=kx
funksiya, y=kx funksiyaning
grafigini yasash, to‘g‘ri
proporsional bog‘lanish va proporsionallik koeffitsiyenti, y=kx funksiyaning grafigini yasashda bir
nuqtaning yetarliligi.
|
|