Natural ko`rsatkichli darajaning xossalari qaralganda darajalarni bo`lishning
an : am = an ─ m (1)
xossasi n > m va a ≠ 0 bo`lganda to`g`riligi ta’kidlangan edi.
Agar n ≤ m bno`lsa, u holda (1) tenglikning o`ng qismidagi n – m daraja ko`rsatkich manfiy son yoki nolga teng bo`ladi.
Manfiy va nol ko`rsatkichli daraja shunday aniqlanadiki, (1) tenglik faqat n > m bo`lgandagina emas, balki n ≤ m bo`lganda ham to`g`ri bo`ladi.
Masalan,
n
= 2,
m
= 5
bo`lganda (1) formula bo`yicha quyidagini hosil qilamiz:
a2 : a5 = a2 ─ 5 = a ─ 3.
Ikkinchi tomondan
Shuning uchun
deb
hisoblanadi.
|
|
1-ta’rif.
Agar
a
≠ 0
va
n
–
natural son bo`lsa, u holda
|
Misollar:
Agar n = m bo`lsa, u holda (1) formula bo`yicha quyidagini hosil qilamiz:
an : an = an ─ n = a0.
Ikkinchi tomondan,
.
Shuning uchun
a0
= 1
deb hisoblanadi.
|
|
2-ta’rif. Agar a ≠ 0 bo`lsa, u holda a0 = 1 bo`ladi. |
Masalan,
30
= 1,
.
Manfiy ko`rsatkichli darajalardan sonni standart shaklda yozishda foydalanilgan.
Masalan,
Natural ko`rsatkichli darajalrning barcha xossalari istalgan butun ko`rsatkichli darajalar uchun ham to`g`ri bo`ladi.
|
|
Istalgan a ≠ 0, b ≠ 0 va istalgan butun n va m lar uchun quyidagi tengliklar to`g`ri: 1. an ∙ am = an + m. 2. (an)m = a nm.
3.
5. (ab)n = an bn. |
Masalan,
n
< 0
bo`lganda
(ab)n = an bn
tenglikning to`g`riligini isbot qilamiz.
n
– butun manfiy son bo`lsin. U holda
n
= – k
(bunda
k –
natural son). Manfiy ko`rsatkichli darajaning ta’rifidan foydalanib,
quyidagini hosil qilamiz:
.
Butun ko`rsatkichli darajalarning boshqa xossalari ham shunga o`xshash isbot qilinadi
Butun ko`rsatkichli darajalarning xossalarini qo`llashga misollar keltiramiz:
1) 4-3 ∙ 411 ∙ 4-6 = 4-3 + 11 – 6 = 42 = 16;
2)
.
Masala.
a6(a-2
– a-4) (a2 + a3)-1
ifodani soddalashtiring:
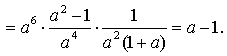
TAYANCH TUSHUNCHALAR:
|
|